给定两个大小分别为 m 和 n 的正序（从小到大）数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。

算法的时间复杂度应该为 O(log (m+n)) 。

示例 1：

输入：nums1 = [1,3], nums2 = [2]
输出：2.00000

解释：合并数组 = [1,2,3] ，中位数 2

示例 2：

输入：nums1 = [1,2], nums2 = [3,4]
输出：2.50000

解释：合并数组 = [1,2,3,4] ，中位数 (2 + 3) / 2 = 2.5

提示：

  • nums1.length == m
  • nums2.length == n
  • 0 <= m <= 1000
  • 0 <= n <= 1000
  • 1 <= m + n <= 2000
  • -106 <= nums1[i], nums2[i] <= 106

大体思路

上来第一种解法当然是熟悉的暴力解法，将两个数组合到一起，然后sort一下，取中位数即可，显然我们知道这种方式并不可取。此时我们需要根据中位数的特性，即在整个数字列表的中间，那么其实我们只要构造出完整列表的前半部分就能取到中位数，再进一步实际上我们只关心最靠近中间的值是多少，对于前半部分的数值仅仅是我们用来获取靠近中间值的途径，所以并不需要保存下来，那么仅仅需要有变量用来保存最靠近中间的值即可，我们并不需要真正保存数组的前半部分。

第二个问题就是到底靠近中间的值指的是什么？对于奇数数量(假设长度为n)的列表，那么中间位置就是 (n + 1) / 2 - 1。而对于偶数数量的列表，中间位置就是 n/2 - 1 和 n/2 的中间。综上，我们仅仅需要遍历 (n+1) / 2 或者 n/2 + 1个数的值即可。比较两个数组里面的值，哪个值更小，就把哪个值塞到新的列表中，接着比较后面的值。

例子

例子1

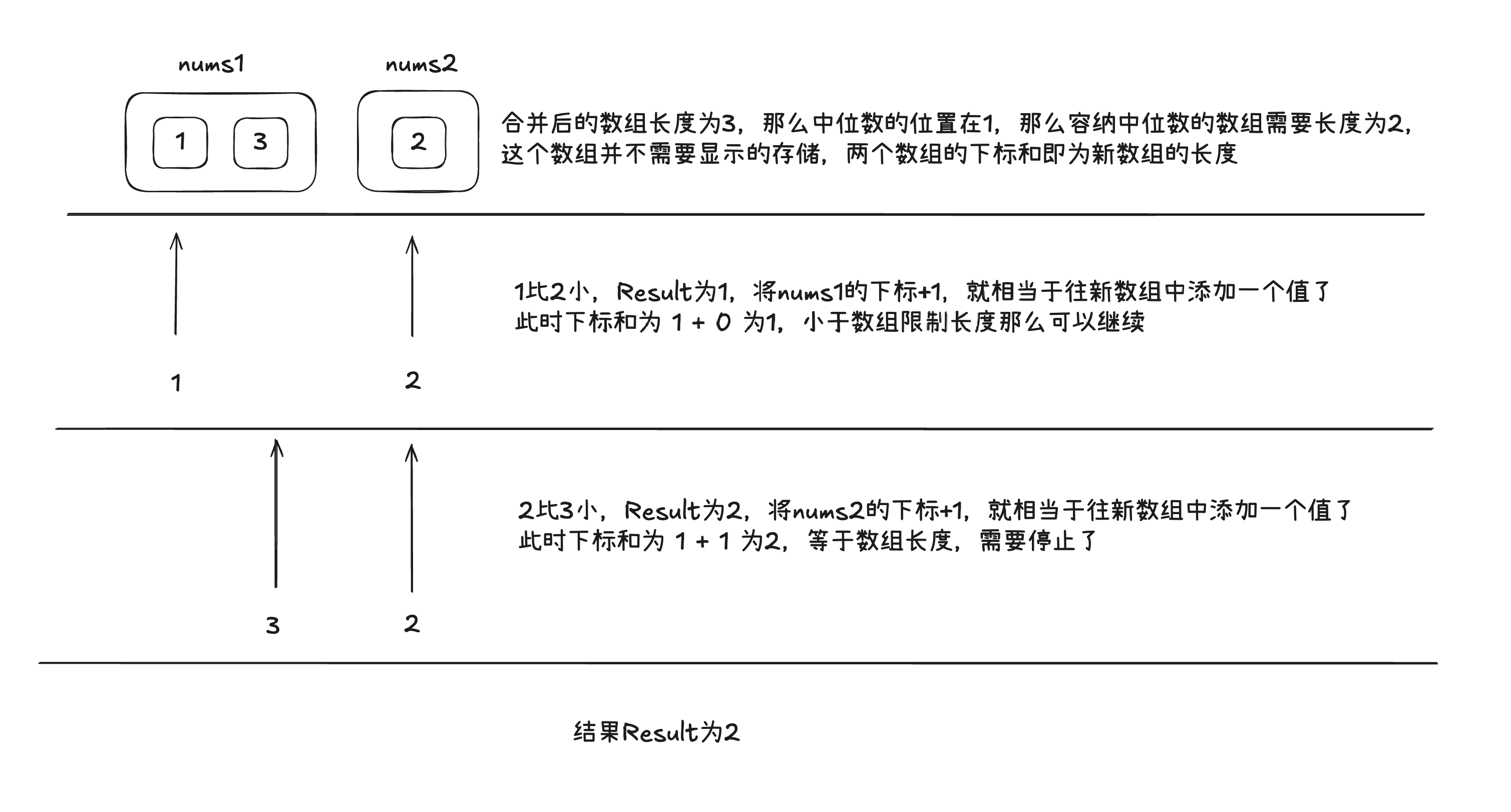
[1,3] 和 [2]， 因为完整数组的长度是3奇数，所以中间位置在 (3 + 1) / 2 - 1即索引1的位置，那么新数组的长度就必须是2(长度比索引大1)，那么按次比较放入新的数组：

  1. nums1[0]为1和nums2[0]为2，1比较小放入新数组中，nums1往后一位，新数组为[1]，数组长度为1，继续
  2. nums1[1]为3和nums2[0]为2，2比较小放入新数组中，nums2往后一位，新数组为[1,2]，数组长度为2，停止

则中位数为2

这里实际我们并不需要实际上构造出新数组，用一个变量存一下结果值，新数组的长度就是两个数组的下标相加，那么简化一下就是：

  1. nums1[0]为1和nums2[0]为2，1比较小，结果值为1，nums1往后一位，数组下标和为1，继续
  2. nums1[1]为3和nums2[0]为2，2比较小，结果值为2，nums2往后一位，数组下标和为2，停止
例子2

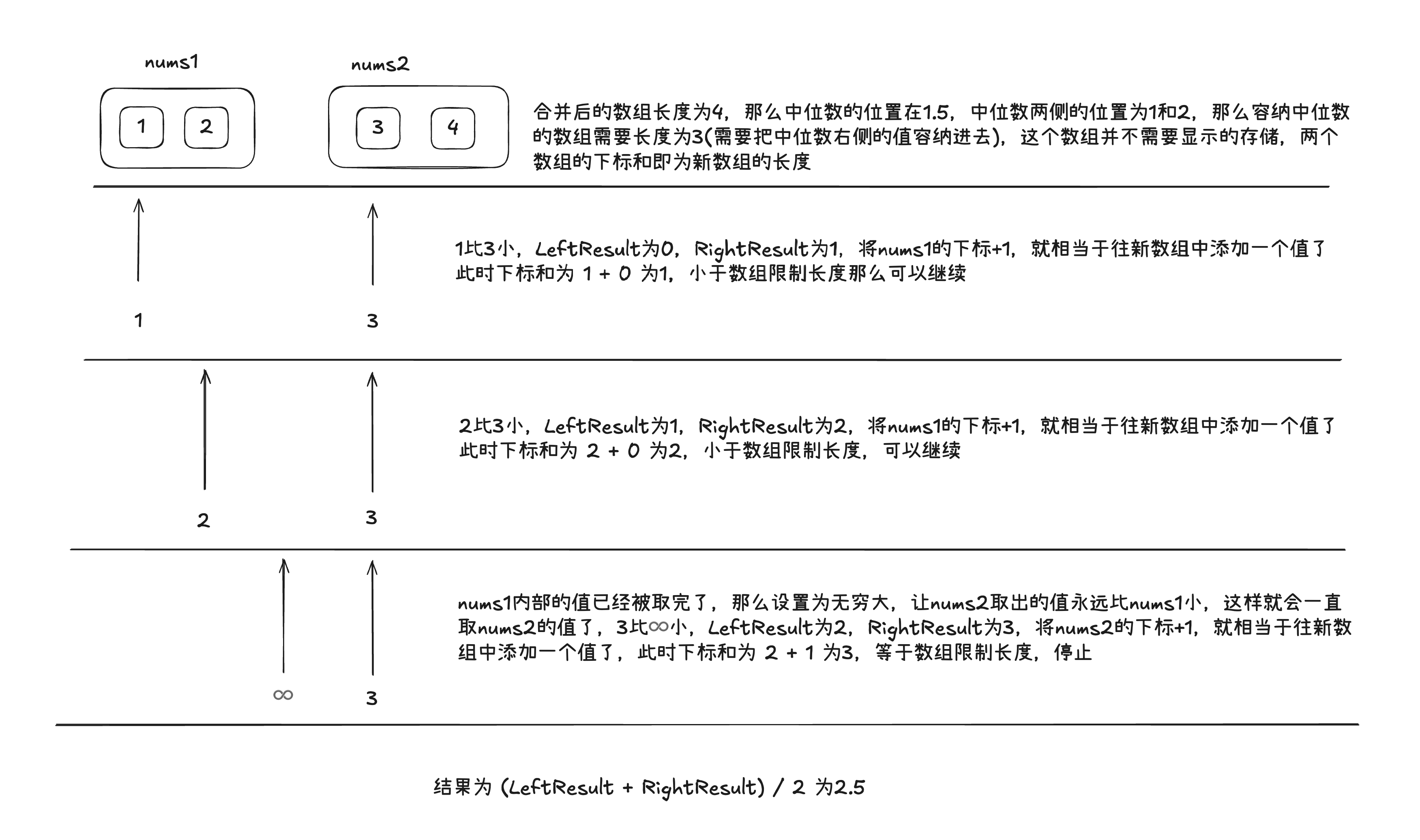
[1,2] 和 [3,4]，完整数组长度为4是偶数，所以中间位置在索引1和索引2之间，这样就需要用两个变量(用leftResult和rightResult，设置初始值为0)来存放结果，新数组的长度为3(即索引最大值 + 1)

  1. nums1[0]为1，nums2[0]为3，1比较小，那么rightResult为1，nums1往后一位，数组下标和为1，继续
  2. nums1[1]为2，nums2[0]为3，2比较小，那么rightResult为2，leftResult为原先rightResult的值1，nums1往后一位，数组下标和为2，继续
  3. (这里需要注意了，nums1数组已经被取完了，那么下面只能再取nums2内的值，所以我们简单起见直接将数组越界的值设置为无穷大，这样比较的时候就会直接去使用nums2内的值)nums1[2]为无穷大，nums2[0]为3，3比较小，那么rightResult为3，leftResult为原先rightResult的值2，nums2往后一位，数组下标和为3，结束

则中位数为 (2 + 3) / 2 为 2.5

代码

var findMedianSortedArrays = function(nums1, nums2) {
    const sumLength = nums1.length + nums2.length  //获取总数组的长度
    const isOdd = sumLength % 2 !== 0 //判断要构造的新列表是奇数还是偶数
    let nums1Pointer = 0
    let nums2Pointer = 0

    //如果是奇数 就取中间的值
    if (isOdd) {
        const newArrLength = (sumLength + 1) / 2
        let result = 0
        
        //下标和没到新数组的长度 就进行循环
        while (nums1Pointer + nums2Pointer < newArrLength) {
            //取出对应数组下标的值进行比较，如果数组越界了就赋值为无穷大，这样就去取另一个数组内的值
            const nums1Value = nums1Pointer >= nums1.length ? Infinity : nums1[nums1Pointer]
            const nums2Value = nums2Pointer >= nums2.length ? Infinity : nums2[nums2Pointer]

            //哪个数值小就将结果设置为哪个值，且将对应的数组下标加1
            if (nums1Value < nums2Value) {
                result = nums1Value
                nums1Pointer++
            }else {
                result = nums2Value
                nums2Pointer++
            }
        }

        //循环完毕result就是中间值
        return result
    } else {
        //如果是偶数 就取中间值两侧的值 求平均数
        const newArrLength = sumLength / 2
        //创建两个变量用于存放中间值两侧的值，leftResult在左边小 rightResult在右边大
        let leftResult = 0
        let rightResult = 0

        //偶数的时候，因为要取到中间值两侧的值，所以长度比奇数大1
        while (nums1Pointer + nums2Pointer < newArrLength + 1) {
            const nums1Value = nums1Pointer >= nums1.length ? Infinity : nums1[nums1Pointer]
            const nums2Value = nums2Pointer >= nums2.length ? Infinity : nums2[nums2Pointer]
            
            //更新中间值两侧的值，leftResult即为上一轮中间值的右侧值，rightResult即为这一轮的小值
            leftResult = rightResult
            if (nums1Value < nums2Value) {
                rightResult = nums1Value
                nums1Pointer++
            }else {
                rightResult = nums2Value
                nums2Pointer++
            }
        }

        //最后中间值两侧值求平均
        return (leftResult + rightResult) / 2
    }

};

图例示意：