给你一个字符串 s，找到 s 中最长的 回文 子串。

示例 1：

输入：s = “babad”
输出：”bab”
解释：”aba” 同样是符合题意的答案。

示例 2：

输入：s = “cbbd”
输出：”bb”

提示：

  • 1 <= s.length <= 1000
  • s 仅由数字和英文字母组成

解题

上来还是最简单的暴力解法，构造若干个子串，然后把这些子串reverse之后看看是不是和原子串一样。再进一步可以将原先整个字符串reverse之后，然后看看这个反转之后的字符串是否包含那些子串。但是这两种解法其实没啥本质上的区别，耗时太长。

回到问题的本质上，回文字符串是什么，简单来说就是轴对称，正反读都是一样的。那么回文字符串就分为两种，一种是奇数回文字符串，如”aba”，一种是偶数回文字符串，如”abba”。这两种我们都只需要从中向外比较，两侧的值是一样的即可。

代码

var longestPalindrome = function(str) {  
    let maxStrLength = 0  //记录最大的回文子串长度
    let maxStart = 0 //记录最大的回文子串是从什么位置开始的
  
    function check(left, right) {
        //当左右都有值的时候，判断这两个字符是不是一致的，如果是一致的，就看再往外一层的
        while (left >= 0 && right < str.length && str.charAt(left) === str.charAt(right)) {
            const length = right - left + 1
            //如果新的回文字符串比之前的长的话，就进行更新
            if (length > maxStrLength) {
                maxStrLength = length
                maxStart = left
            }
            left--
            right++
        }
    }
    
    //遍历
    for (let i = 0; i < str.length; i++) {
        //以i为中心，向两侧扩展
        check(i, i)
        //以i和i+1为中心，向两侧扩展
        check(i, i+1)
    }
    
    //得到最大的子串
    return str.substring(maxStart, maxStart + maxStrLength)
};

代码演示

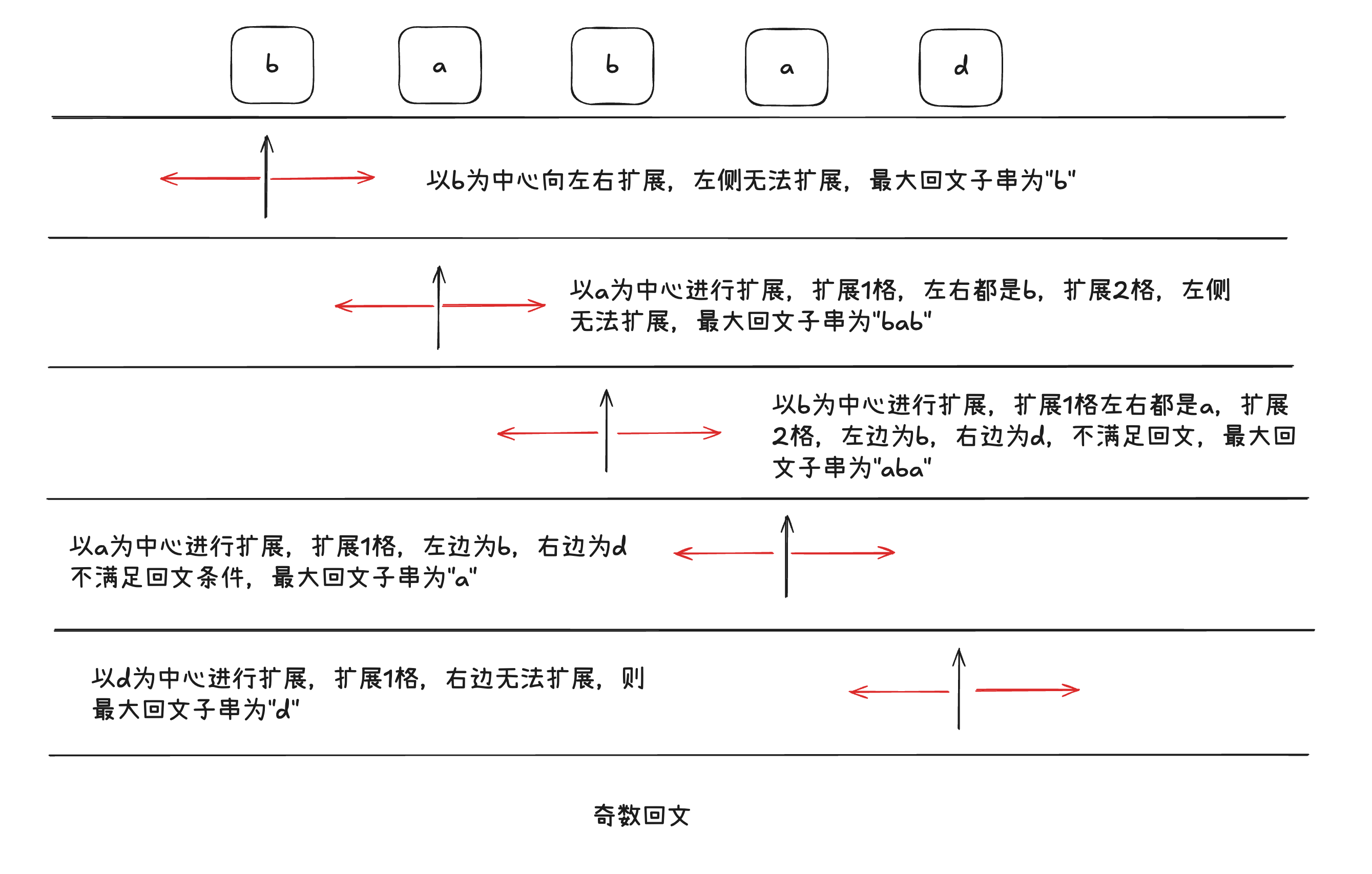
示例1 “babad”
  • index = 0
    • 奇数回文，以b为中心，向外扩展
      1. 向外0长度，子串为”b”，满足回文字符串，最大回文子串为”b”
      2. 向外1长度，左边无法扩展
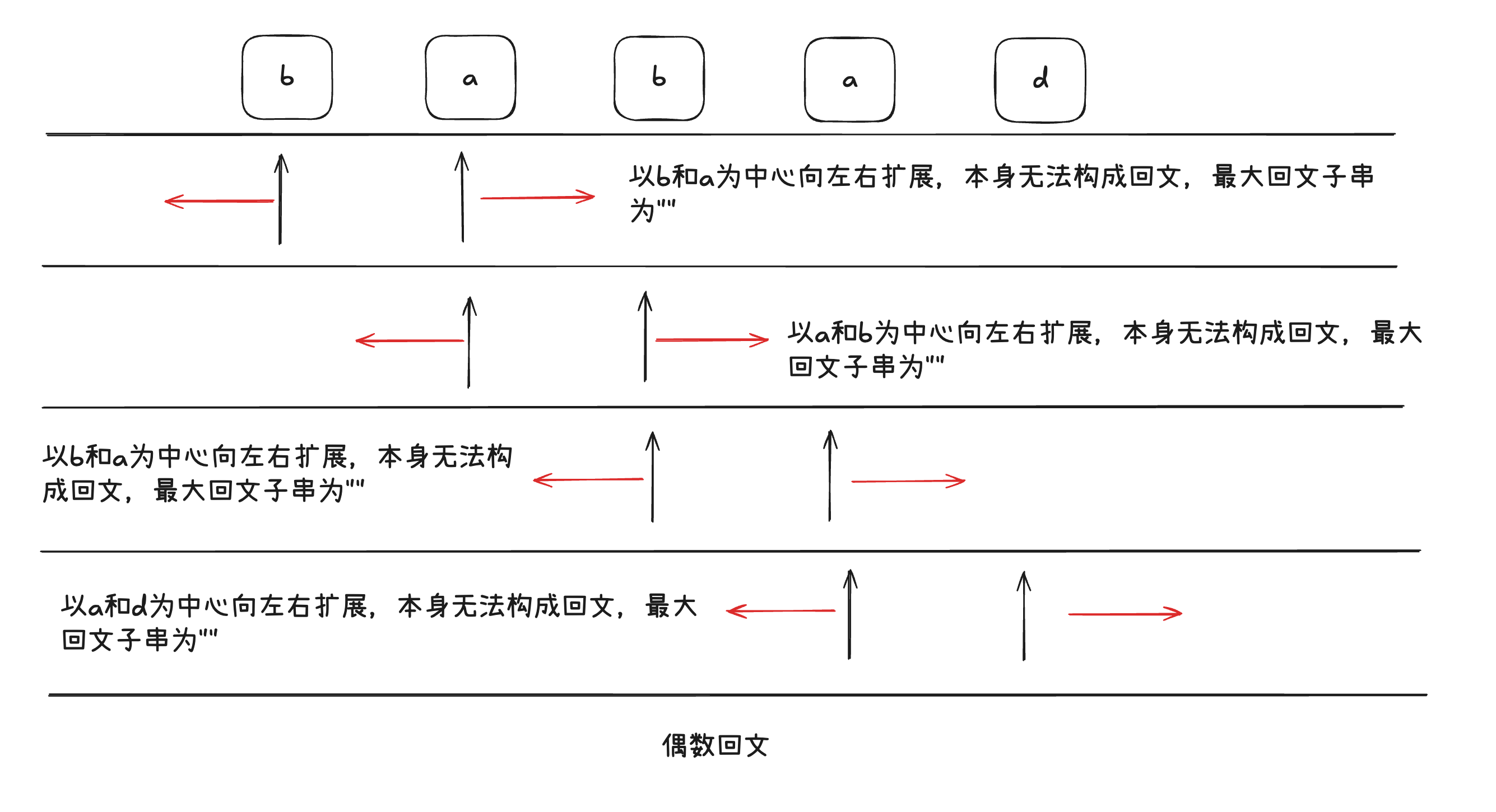
    • 偶数回文，以b和a为中心，向外扩展
      1. 向外0长度，左边为b，右边为a，子串为”ba”，不满足回文字符串
  • index = 1
    • 奇数回文，以a为中心，向外扩展
      1. 向外0长度，子串为”a”，满足回文字符串，最大回文字符串为”a”
      2. 向外1长度，左边为b，右边也为b，子串为”bab”，满足回文字符串，最大回文字符为”bab”
      3. 向外2长度，左边无法扩展
    • 偶数回文，以a和b为中心，向外扩展
      1. 向外0长度，左边为a，右边为b，子串为”ab”，不满足回文字符串
  • index = 2
    • 奇数回文，以b为中心，向外扩展
      1. 向外0长度，子串为”b”，满足回文字符串，最大回文字符串为”b”
      2. 向外1长度，左边为a，右边也为a，子串为”aba”，满足回文字符串，最大回文字符为”aba”
      3. 向外2长度，左边为b，右边也为d，子串为”babad”，不满足回文字符串
    • 偶数回文，以b和a为中心，向外扩展
      1. 向外0长度，子串为”ba”，不满足回文字符串
  • index = 3
    • 奇数回文，以a为中心，向外扩展
      1. 向外0长度，子串为”a”，满足回文字符串，最大回文字符串为”a”
      2. 向外1长度，左边为b，右边也为d，子串为”bad”，不满足回文字符串
    • 偶数回文，以a和d为中心，向外扩展
      1. 向外0长度，子串为”ad”，不满足回文字符串
  • index = 4
    • 奇数回文，以d为中心，向外扩展
      1. 向外0长度，子串为”d”，满足回文字符串，最大回文字符串为”d”
      2. 向外1长度，右侧无法扩展
    • 偶数回文，右侧超出字符串长度

结论最大子回文字符串为”bab”和”aba”


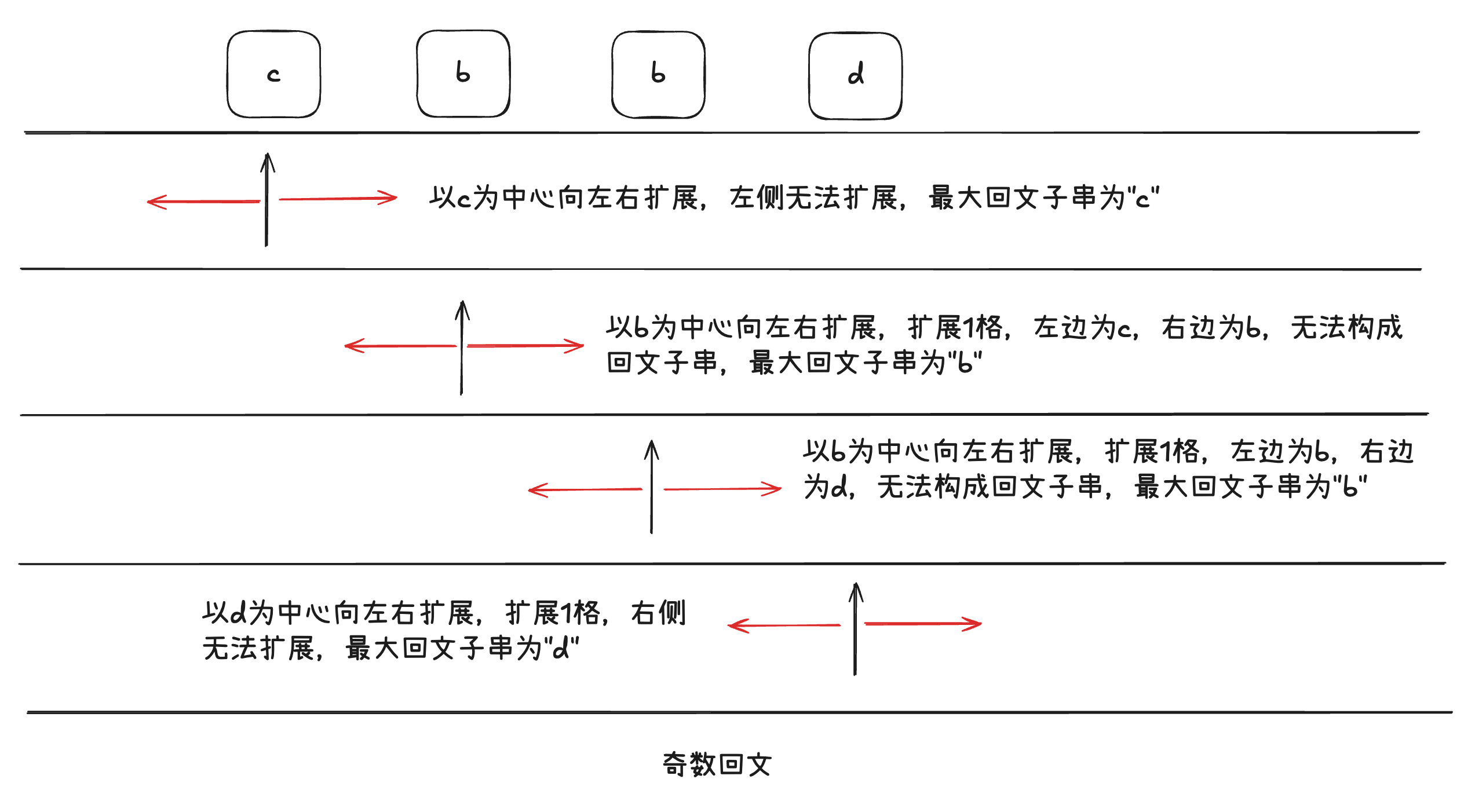
示例2 “cbbd”
  • index = 0
    • 奇数回文，以c为中心，向外扩展
      1. 向外0长度，子串为”c”，满足回文字符串，最大回文字符串为”c”
      2. 向外1长度，左侧无法扩展
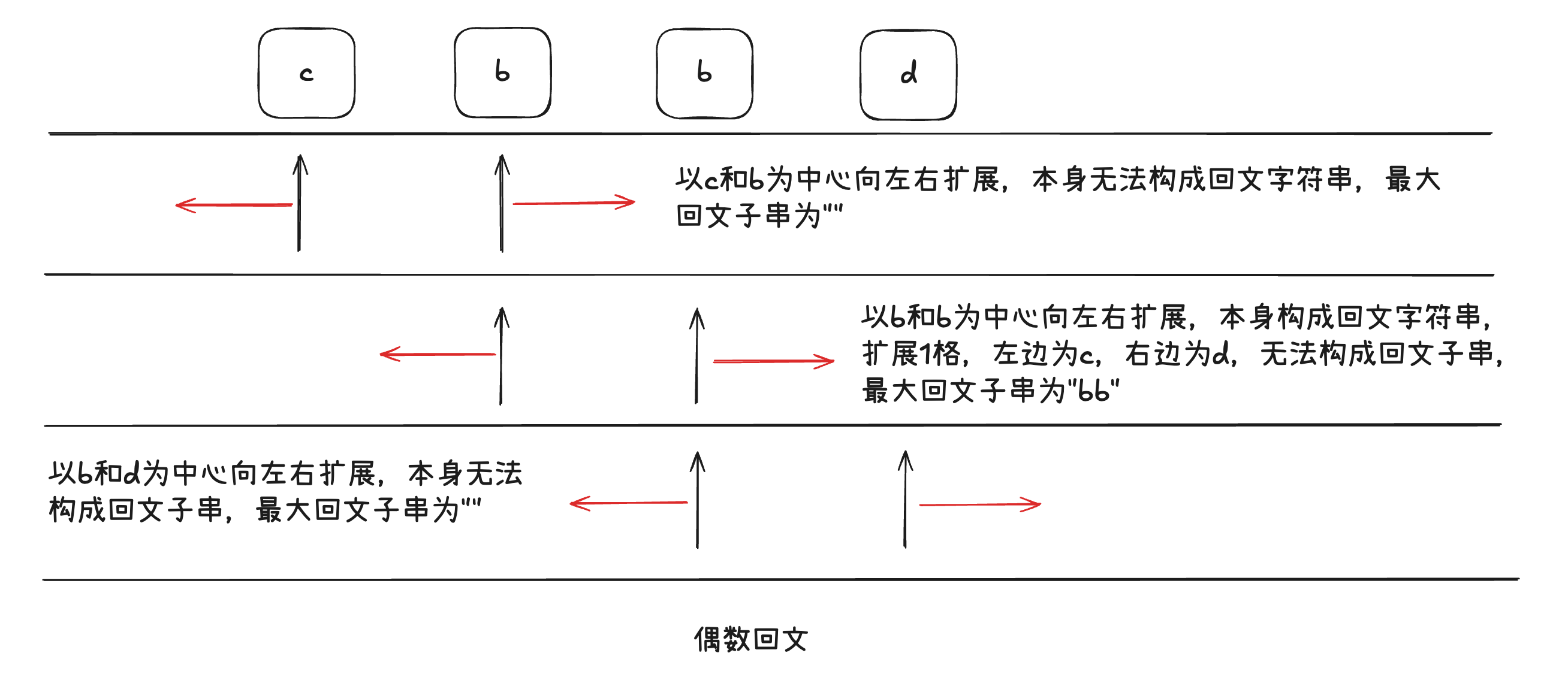
    • 偶数回文，以c和b为中心，向外扩展
      1. 向外0长度，子串为”cb”，不满足回文字符串
  • index = 1
    • 奇数回文，以b为中心，向外扩展
      1. 向外0长度，子串为”b”，满足回文字符串，最大回文字符串为”b”
      2. 向外1长度，左边为c，右边为b，子串为”cbb”，不满足回文字符串
    • 偶数回文，以b和b为中心，向外扩展
      1. 向外0长度，子串为”bb”，满足回文字符串，最大回文子串为”bb”
      2. 向外1长度，左边为c，右边为d，不满足回文字符串
  • index = 2
    • 奇数回文，以b为中心，向外扩展
      1. 向外0长度，子串为”b”，满足回文字符串，最大回文字符串为”b”
      2. 向外1长度，左边为b，右边为d，子串为”bbd”，不满足回文字符串
    • 偶数回文，以b和d为中心，向外扩展
      1. 向外0长度，子串为”bd”，不满足回文字符串
  • index = 3
    • 奇数回文，以d为中心，向外扩展
      1. 向外0长度，子串为”d”，满足回文字符串，最大回文字符串为”d”
      2. 向外1长度，右侧无法扩展
    • 偶数回文，右侧超出字符串长度

结论最大回文字符串为”bb”


额外说明

现在使用的这种“中间扩展法”依旧不是最优解，可以看到在进行奇数回文和偶数回文的判断过程中，有很多重复的判断，这导致了时间的浪费，问题的原因在于需要根据中心是奇数还是偶数分开判断。有一种Manacher算法，是专门针对回文的算法，但是这里不展开，仅仅提一嘴，它通过往字符串中添加特殊字符，来让字符串都变为奇数字符串，如:

“babad” -> “#b#a#b#a#d#”

“cbbd” -> “#c#b#b#d#”

这样就解决了需要分别判断的问题。