给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。

找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

返回容器可以储存的最大水量。

说明：你不能倾斜容器。

示例 1：

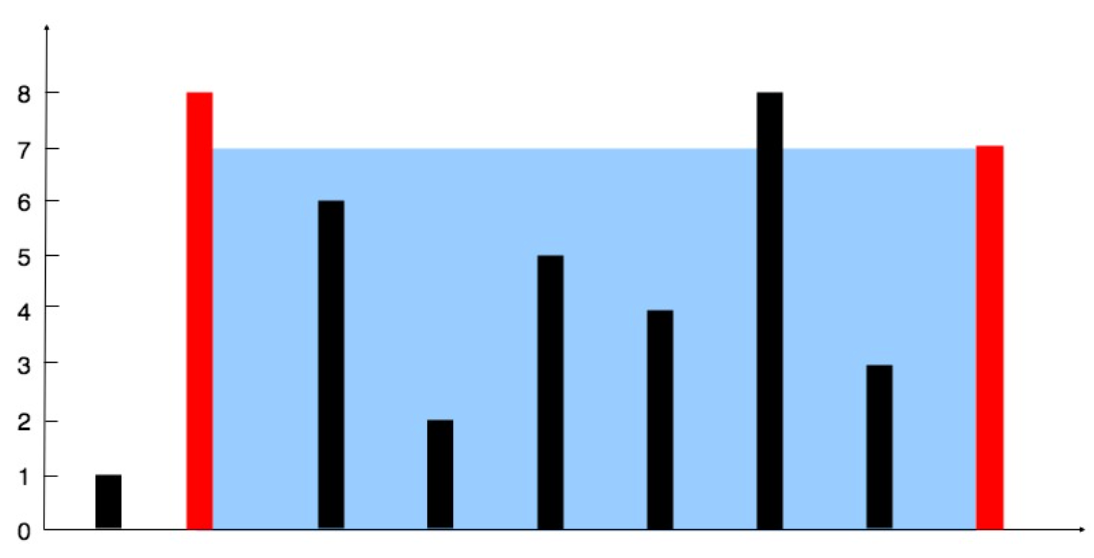
输入：[1,8,6,2,5,4,8,3,7]

输出：49

解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

示例 2：

输入：height = [1,1]

输出：1

提示：

  • n == height.length
  • 2 <= n <= 105
  • 0 <= height[i] <= 104

解题思路

这题看上去很难，其实简化一下非常简单，求所能盛水的最大容器，其实就是求X轴和Y轴所能构成的矩形的最大面积，那就需要两个要求:

  • X轴上两根垂直线尽可能离得够远，即宽度够大
  • Y轴上两根垂直线的高度尽可能大，即高度够大

那么我们一上来就将两根垂直线放到相距最远的位置，这样就解决了X轴需要距离尽可能远的要求。让line1从左边往中间靠，让line2从右边往中间靠，在两根线往中间靠的过程中，如果新的垂直线的高度小于当前的高度，那么就可以直接跳过。

因为矩形在X轴的值在垂直线向中间靠拢的过程中变小了，那么想要得到更大的矩形，就意味着只能让Y轴上能更大，才有可能构造出更大的矩形。然后进行面积的比较，如果新的面积大，那就记录下此时两根垂直线的高度，作为新的基准。然后比较左右两根垂直线，高度低的线向中间推。

演示流程

输入：[1,8,6,2,5,4,8,3,7]

  1. 初始设置，面积areaMax=0，左侧垂直线指针left=0，右侧垂直线指针right=length-1，左侧最大高度leftHeight=0，右侧最大高度rightHeight=0
  2. 查看两根线是否重叠，right为8，left为0，继续
  3. 当前左侧高度1，当前右侧高度7，均大于最大左侧、最大右侧高度，当前面积为(8 - 0) * 1 = 8，大于最大面积。将最大面积设置为8，最大左侧高度设置为1，最大右侧高度设置7
  4. 比较左右两侧高度，移动小的那一侧，即左侧，left++
  5. 查看两根线是否重叠，right为8，left为1，继续
  6. 当前左侧高度8，大于最大左侧高度，当前面积为(8 - 1) * 7 = 49，大于最大面积。将最大面积设置为49，最大左侧高度设置为8，最大右侧高度设置为7
  7. 比较左右两侧高度，移动小的那一侧，即右侧，right--
  8. 查看两根线是否重叠，right为7，left为1，继续
  9. 当前左右两侧高度均小于等于最大左右两侧最大高度，跳过
  10. 比较左右两侧高度，移动小的那一侧，即右侧，right--
  11. 查看两根线是否重叠，right为6，left为1，继续
  12. 当前右侧高度大于最大右侧高度，当前面积为(6 - 1) * 8 = 40，小于最大面积，跳过
  13. 比较左右两侧高度，移动小的那一侧，即左侧，left++
  14. 查看两根线是否重叠，right为6，left为2，继续
  15. 当前左右两侧高度均小于等于最大左右两侧最大高度，跳过
  16. 比较左右两侧高度，移动小的那一侧，即左侧，left++
  17. 查看两根线是否重叠，right为6，left为3，继续
  18. 当前左右两侧高度均小于等于最大左右两侧最大高度，跳过
  19. 比较左右两侧高度，移动小的那一侧，即左侧，left++
  20. 查看两根线是否重叠，right为6，left为4，继续
  21. 当前左右两侧高度均小于等于最大左右两侧最大高度，跳过
  22. 比较左右两侧高度，移动小的那一侧，即左侧，left++
  23. 查看两根线是否重叠，right为6，left为5，继续
  24. 当前左右两侧高度均小于等于最大左右两侧最大高度，跳过
  25. 比较左右两侧高度，移动小的那一侧，即左侧，left++
  26. 查看两根线是否重叠，right为6，left为6，已经重叠，结束流程，最大面积49

代码实现

/**
 * @param {number[]} height
 * @return {number}
 */
var maxArea = function(height) {
    //左侧垂直线指针
    let left = 0
    //右侧垂直线指针
    let right = height.length - 1
    //最大面积
    let areaMax = 0
    //左侧垂直线最大高度
    let leftHeight = 0
    //右侧垂直线最大高度
    let rightHeight = 0

    //如果两侧线没有重叠
    while (right >= left) {
        //获取当前垂直线高度
        const currentLeft = height[left]
        const currentRight = height[right]

        //如果有一侧的高度大于最大高度，那么进行面积测量
        if (leftHeight < currentLeft || rightHeight < currentRight ) {
            //计算面积，跟最大面积进行比较，如果大于最大面积的话，更新左右最大高度
            const area = (right - left) * Math.min(currentLeft, currentRight)
            if (area > areaMax) {
                areaMax = area
                leftHeight = currentLeft
                rightHeight = currentRight
            }
        }

        //进行左右两侧高度比较，移动小的那一侧
        if (currentLeft <= currentRight) {
            left++
        }else {
            right--
        }
    }

    return areaMax
};