给你一个整数数组 nums ，判断是否存在三元组
[nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k
同时还满足 nums[i] + nums[j] + nums[k] == 0 。请你返回所有和为 0 且不重复的三元组。

注意：答案中不可以包含重复的三元组。

示例 1：
输入：nums = [-1,0,1,2,-1,-4]
输出：[[-1,-1,2],[-1,0,1]]
解释：
  nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0 。
  nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0 。
  nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0 。
不同的三元组是 [-1,0,1] 和 [-1,-1,2] 。
注意，输出的顺序和三元组的顺序并不重要。

示例 2：
输入：nums = [0,1,1]
输出：[]
解释：唯一可能的三元组和不为 0 。

示例 3：
输入：nums = [0,0,0]
输出：[[0,0,0]]
解释：唯一可能的三元组和为 0 。
 

提示：

3 <= nums.length <= 3000
-105 <= nums[i] <= 105

解题思路

刚拿到这一题，第一个想法是暴力循环，拼出nums[i] + nums[j] + nums[k] = 0，但是这样最后得出的结果就是超出时间限制。第二个想法是两数之和的延伸，先创建一个Map，将0 - nums[i]存到map中，然后双循环之后将sum与map中的Key进行比较，发现仍旧还是超出时间限制。
那接下来需要考虑的事就是减少循环的次数，我们知道三数之和要等于0的话，那么说明要么三数都是0，要么就是有正负之分。那么我们先将nums进行排序，然后选择一个位置i作为基准，如果nums[i]大于0的话，那么nums[i]右边的值就不用进行遍历了，因为最小值都已经大于0了。这时我们设置两个指针，一个在最左边，一个在最右边，这样可以根据三数之和与0的大小关系就可以进行对应的调整。

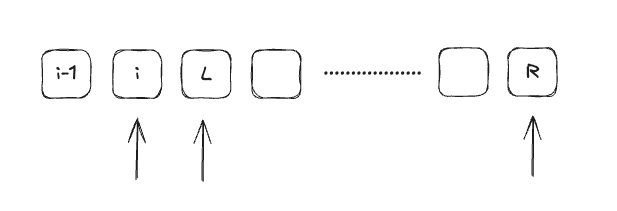
如果nums[i] + nums[L] + nums[R] > 0的话，说明应该减少一点，那么我们就将R--，如果小于0，说明应该增加一点，那么我们就将L++。然后还有一些重复的点，比如nums[i] + nums[L] + nums[R] > 0且此时如果nums[R] === nums[R--]那么就可以跳过R，那么一直R--，直到nums[R] !== nums[R-x]，L也是一样的道理，且i也是类似的，如果nums[i - 1] === nums[i]，说明是重复的，可以跳过。

代码

var threeSum = function(nums) {
    let result = []

    nums.sort((a, b) => a - b)

    for (let i = 0; i < nums.length; i++) {
        if (nums[i] > 0) break  //最小的值大于0，直接退出

        if (i > 0 && nums[i] === nums[i-1]) continue //如果nums[i] === nums[i-1]说明重复，可以跳过

        let L = i + 1

        let R = nums.length - 1

        while(L < R) {
            let sum = nums[i] + nums[L] + nums[R]
            if (sum === 0) {
                result.push([nums[i], nums[L], nums[R]])
                while (L < R && nums[L] === nums[L+1]) L++ //如果L+1的值和L一样，那么可以跳过
                while (L < R && nums[R] === nums[R-1]) R--
                L++
                R--
            }else if (sum < 0){
                L++
            }else {
                R--
            }
        }
    }

    return result
};