给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。答案可以按 任意顺序 返回。

给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。

示例 1：
输入：digits = "23"
输出：["ad","ae","af","bd","be","bf","cd","ce","cf"]

示例 2：
输入：digits = ""
输出：[]

示例 3：
输入：digits = "2"
输出：["a","b","c"]
 

提示：
0 <= digits.length <= 4
digits[i] 是范围 ['2', '9'] 的一个数字。

解题思路

简单的方式就是进行遍历，按照示例1来说，就是遍历’2’对应的三个字符，并在这三个字符后拼上’3’对应的三个字符，依次类推。

将对应的数据结构拼凑出来，很明显可以看出是个树形结构，而我们需要得到的结果，就是所有的叶子节点。那么就产生了两种做法:

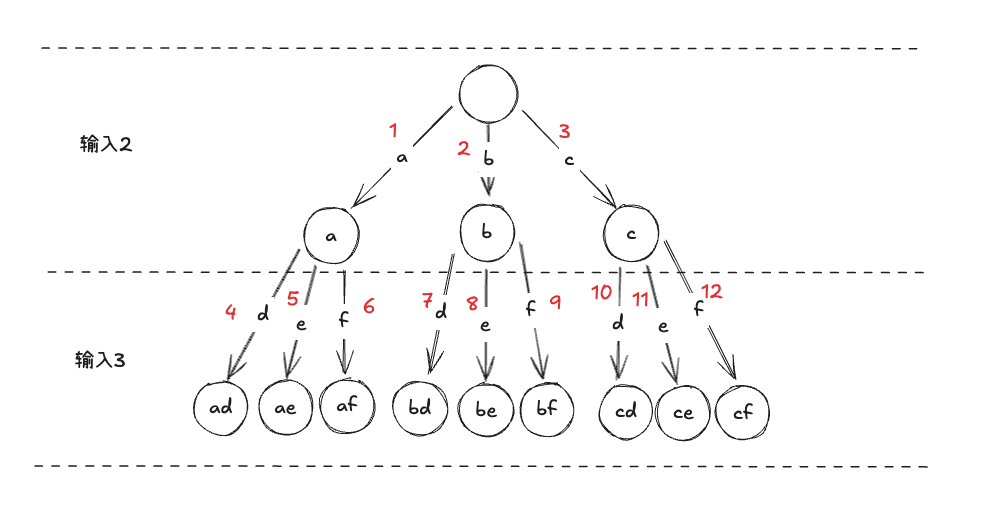
  1. 广度优先(从根节点出发，每一层都把所有的节点都得到后，再继续往下层遍历，直到获取到最底层)
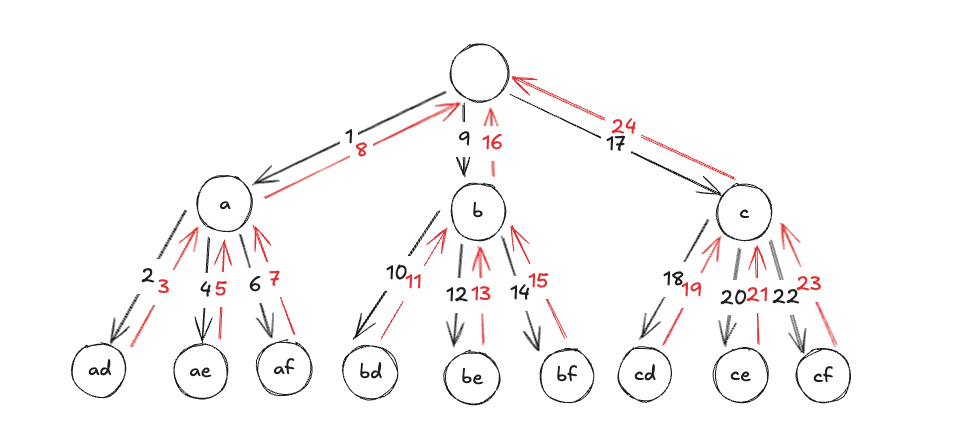
  2. 深度优先(从根节点出发，直到得到一个叶子节点后，返回上一层，获取另一个叶子节点，这种行为称之为回溯)

广度优先做法

var letterCombinations2 = function (digits) {
  if (digits === '') {  //如果digits为空，那么直接返回[]
    return []
  }

  //设置一个map，用于映射按下的数字与字符的关系
  const charMap = {
    2: ['a', 'b', 'c'],
    3: ['d', 'e', 'f'],
    4: ['g', 'h', 'i'],
    5: ['j', 'k', 'l'],
    6: ['m', 'n', 'o'],
    7: ['p', 'q', 'r', 's'],
    8: ['t', 'u', 'v'],
    9: ['w', 'x', 'y', 'z'],
  }

  function getMapChar(d, rArr) {
    //获取当前数字对应的字符列表
    const dArr = charMap[d]
    const newArr = []
    //双循环，将已遍历节点的内容，拼上数字对应的字符列表
    for (let i = 0; i < dArr.length; i++) {
      for (let j = 0; j < rArr.length; j++) {
        newArr.push(`${rArr[j]}${dArr[i]}`)
      }
    }
    return newArr
  }

  let result = ['']
  for (let i = 0; i < digits.length; i++) {
    //获取每一层的节点内容
    //[]
    //['a', 'b', 'c']
    //['ad','ae', 'af', 'bd', 'be', 'bf', 'cd', 'ce', 'cf']
    result = getMapChar(digits.charAt(i), result)
  }

  return result
}

深度优先做法

var letterCombinations = function (digits) {
  //设置数字对应的字符数组，包含了 0，1 这种不对应任何字符的数字
  const map = ['', '', 'abc', 'def', 'ghi', 'jkl', 'mno', 'pqrs', 'tuv', 'wxyz']
  //如果没有输入任何数字，则返回[]
  if (!digits.length) return []
  //如果输入的数字长度为1，那么直接将对应的字符切成数组返回即可
  if (digits.length === 1) return map[digits].split('')

  //res存放结果
  //path存放遍历路径的节点值
  const res = [], path = []
 
  function backtracking(index) {
    //如果当前已经遍历完了最深的层级，那么这条路径的字符数组合并就是对应的最深层叶子节点对应的值 如['a', 'd'] ---> ['ad']
    if (index === digits.length) {
      res.push(path.join(''))
      return
    }
    //遍历输入数字对应的字符
    for (const v of map[digits[index]]) {
      //将当前的字符放入path中
      path.push(v)
      //查看更深层
      backtracking(index + 1)
      //最深层已经获取到了，返回上一个父节点, 开始遍历父节点的下一个子节点
      path.pop()
    }
  }

 
  backtracking(0)
  return res
}